현대 인식론 입문 수업에서 자연 법칙(Laws of Nature)에 대한 스탠포드 철학 백과사전 항목을 요약 발제한 내용이다.
전공 분야가 아니어서 이해하는 데 어려움을 겪었다. 틀린 이해가 많을 수 있다.
이 글을 바탕으로 한 자세한 글은 나중으로 기약해본다.
자연 법칙과 우연적 일반화를 구분짓는 기준.
법칙의 조건
- 과학적 실천에서 중심적 역할 수행
- 다른 철학적 문제에서도 중요한 영향
– 반사실적 설명이 참이 되는 경우, 법칙과 비법칙을 가르는 기준 등 - 연역적 추론에 의한 확증성(confirmability)과 연계된 법칙다움(lawhood) (Goodman, 1947)
- 우연적으로 참인 일반화와 구별
– “지금 모두가 다 앉아 있다” = 우연적 일반화 = 비법칙적 = “모든 순금구(球)는 지름이 1 마일 보다 작다(All gold spheres are less than a mile in diameter)”
– 상대성 이론, “빛보다 빠른 신호는 없다” = 참인 일반화 = “모든 우라늄구는 지름이 1 마일 보다 작다(All uranium spheres are less than a mile in diameter)”
체계(Systems)
- 체계 접근(Systems approach): 우연적 일반화와 법칙을 구분하는 기준
– 연역 체계(deductive systems): 공리들로 개별화(individuate)되는 논리적 체계. 강건성(strength)과 단순성(simplicity)이라는 덕을 갖고 있음. 모든 공리를 포함하면 가장 강건한 체계가 되는 반면, 단 하나의 공리만 포함하면 가장 단순한 체계가 됨.
– 법칙: 강건성과 단순성이 최고의 조합(the best combination)을 이루는 참인 연역 체계.
– 우라늄구 명제가 법칙인 이유는, 우주에 관한 이론 중 양자역학이 최고의 체계(the best system)를 이루는데, 이 명제가 양자역학과 함께 우라늄의 속성을 잘 설명하기 때문. 반면 순금구 명제는 어떤 체계의 공리에 적용되더라도 강건성이나 단순성에 영향을 미치지 못함. - 체계 접근에 대한 비판
– 체계 접근은 실질적 법칙에서 공허한 진리(vacuous truth)를 배제할 수 없음. 공허한 진리: (P → Q) ∧ (P = Φ) ⇒ Q. “모든 유니콘은 미혼이다.”
– 체계 접근은 ‘과학의 목적은 법칙의 발견’이라는 뻔한 소리로 귀결되기도 함.
– 체계 접근은 루이스(Lewis)가 흄적 수반(Humean supervenience)을 옹호하는 주된 입장.
– 흄적 수반: “세상에 존재하는 모든 것은 특수한 사실들이 국지적으로 형성한 물질들의 모자이크(a mosaic of local matters of particular fact)” - 체계 접근에 대한 기타 비판
– 법칙은 심리의존적(mind-dependent)이라는 주장. 예화하는 능력은 인지 능력에 의존함.
– 존 로버츠(John Roberts), “더 나은 연역 체계를 택하기 위해 서로 경쟁하는 단순성과 정보 내용 중 가중치를 어디에 둘지 연습한 적이 없다” = 단순성을 희생하고 정보를 첨가하여 강력한 체계를 구성해도 무방함. → 필연성을 부정하는 흄적 제약(Humean constraints)을 종종 만족함으로써 필연성을 인정하는 과학적 실재론과 모순됨.
보편자(Universals)
- 보편자 접근(Universals approach): 체계 접근과 흄 주의자(Humean)에 대항해 1970년대 암스트롱(David Armstrong)을 필두로 제기된 새로운 주장.
- 암스트롱의 주장, “Fs가 Gs라는 법칙이 있을 때, F-ness와 G-ness는 보편자이다. F-ness와 G-ness 사이의 특정한 관계, 즉 비논리적이거나 우연적 필연화(contingent necessitation)인 관계가 있다면 N(F,G)로 기호화 할 수 있다.”
– 우라늄 구와 순금 구의 차이를 만드는 것은 ‘우라늄으로 있는 것이 1 마일보다 지름이 작도록 필연화한다’는 것.
– 법칙은 귀납적 추론에서 설명적 역할을 수행한다는 주장. → 심리 의존성 극복 가능, 흄적 수반을 부정. - 바스 반 프라센(Bas van Frassen)의 동일성 문제(the identification problem), “N이 무엇이 됐든, N(F,G)와 Fa일 때 Ga가 절대적으로 불가능하다는 가능성이 보이지 않는다. 암스트롱의 용어 사용법이 어려운데, 그는 법칙화하는 보편자 N을 ‘필연화한다’고 명명했다. N이 필연적 연결관계의 필요조건에 부합하는 경우에만 ‘보편화’라는 이름을 쓸 수 있다. 이름만 가지고는 조건을 만족할 수 없다. ‘Armstrong’이라는 이름을 썼다고 해서 강력한 이두근을 가졌다고 할 수는 없기 때문이다.”
– 법칙화하는 관계가 어떤 관계인지 밝혀야 하고, 그 관계가 법칙화하는 데 적절한지 판단해야 하는 문제 남음. - 암스트롱의 답변, “[법칙화하는 관계를 밝히기 위해] 필요한 관계는 인과적 관계(causal relation)이며, 이 관계는 개별자(token)가 아니라 유형(type)을 연관시킨다.”
– 개별적 사건과 보편자를 연관시키는 인과적 관계가 무엇인지에 대한 문제 남음.
흄적 수반(Humean Supervenience)
- 수반 문제: [모든 사건이 연결되어 있기보다 결합되어 있다(conjoined not connected)는] 흄의 생각은 법칙을 판별하는 기준이 되는가?
- 툴리(Tooley)의 논변: “10 가지의 입자가 있다고 가정해보면, 입자들 사이의 상호작용은 총 55가지가 나온다. 그중 54가지를 확인했고, 입자 X와 입자 Y의 상호작용은 아직 연구되지 않았다. 그 입자들이 상호작용하지 않는 조건이었기 때문이다. 그럼에도 불구하고 입자 X와 Y가 상호작용하여 P나 Q가 발생한다면, 법칙이 될 수 있는 것처럼 보인다. 이러한 일반화들로 법칙이 되도록 고정하는 입자 수준의 국소적인 사항(the local matters of particular fact)은 없는 것 같다.”
- 외로운 입자(lone particle)의 사례: 뉴턴 법칙이 적용되는 빈 공간에서 1m/s로 등속운동하는 유일한 입자를 가정해보면, “모든 물체는 1m/s이다”라는 명제는 우연적 일반화가 되지만, 뉴턴 법칙 대신 모든 물체가 1m/s인 법칙이 작용하는 공간을 가정해보면 다른 입자가 충돌하더라도 우연적 일반화가 아니게 됨.
- 마우들린(Maudlin)의 논변: “특수상대성의 시공간인 민코프스키 시공간은 비어 있을 경우 일반상대성 법칙이 적용된다. 그러나 민코프스키 시공간은 일반상대성 법칙의 유일한 모델이 아니다. 누군가는 비어 있는 민코프스키 시공간을 모델로 특수상대성 법칙이 완벽히 적용되는 시공간 구조를 가정해 새로운 중력 이론을 만들 수도 있다. 일반상대성 법칙이 적용되지 않는 가능세계를 가정할 때, 완전히 물리적인 세계는 법칙을 결정할 수 없다.”
– 법칙은 물질에 수반. 물질 없는 세계에서는 모순되는 두 가지 중력 법칙이 공존할 가능성이 있음.
– 흄 주의자들은 비수반(nonsupervenience)의 불합리성에 노출됨. - 흄 주의의 비수반론 비판, “가능세계는 실제로 가능하지 않다”
– 법칙의 지배성에 관한 헬렌 비비(Helen Beebee)의 의견, “정신의 지배 개념에 대한 논쟁에서 반수반적(antisupervenience) 사례들을 설득적이라고 여기기 쉽지만 흄 주의자들의 법칙성(lawhood)을 거부하기 위해 이 개념을 사용하는 것은 선결문제 요구의 오류이거나 다른 방식으로 설득적이다. 흄 주의자들이 거부한 것이기 때문이다.”
– 인식론, 존재론에 관한 의견, “비수반적 법칙은 개체 아래 놓여있다” - 언어의 작동방식에 관한 로버츠(Roberts)의 의견, “외로운 입자의 사례를 가정하는 순간, 모든 입자가 1m/s로 등속운동하는 법칙이 존재하는 세계와 존재하지 않는 세계가 동시에 제시되며 그 둘은 수반과 모순되지 않는다.” ‘-는 법칙이다(is a law)’라는 술어의 맥락 감수성(context sensitivity)이 달라지기 때문. 진리값이 맥락에 따라 결정됨.
– “모든 입자는 1m/s로 등속운동한다는 것은 법칙이다”가 참이기 위해서는 “모든 입자는 1m/s로 등속운동한다”는 절이 주요 이론(salient theory)에서 법칙적 역할을 수행해야 함.
– 법칙적 역할은 다른 이론과 상대적이며 맥락에 따라 주요 이론이 달라질 수 있으므로 맥락에 종속됨.
– 단일한 일반화는 법칙적 역할을 할 수 없으므로 다른 주요 이론과 맥락이 필요함.
– 법칙성을 결정하는 데 맥락 감수성이 중요.
반실재주의(Antirealism)
- 실재주의: “무엇이 법칙인지 설명하는 것은 실재를 설명한다.” 실재주의에 반대하는 반실재주의.
- 반실재주의의 입장들
– 반 프라센(van Fraassen): “체계 접근과 보편자 접근은 법칙을 허락하는 적절한 인식론을 서술하는 데 실패”
– 로널드 기어리(Ronald Giere): “과학사에서 법칙 개념의 기원을 봤을 때 법칙으로 묘사되는 대부분의 일반화는 거짓”
– 스티븐 멈포드(Stephen Mumford): “지배하기 위해 법칙은 지배되는 속성들 외부에 있어야 하나, 법칙이 외부에 있으면 그 속성들은 정체성을 잃게 됨.”
– ‘빛보다 빠른 신호는 없다’고 했을 때, 이 진술의 법칙성 여부는 세계를 기술하는 사실과 무관. 일반화는 예언과 설명적 역할만 수행. - 법칙성 없는 실재는 반사실적 조건(the counterfactual conditional), 경향(disposition), 인과(causation)와 같은 법적 개념(the nomic concepts)과 연관됨.
– ‘성냥불 붙이기’ 사례: 우리는 정상적인 상황인 경우 최소한 한 가지 이상의 자연 법칙이 있을 것이라 생각하기 때문에, 성냥을 그으면 불이 붙을 것이라 예상함. 이러한 반사실적 조건은 사실임. 왜냐하면 법칙이 없다면 성냥은 불 붙을 경향이 있다(disposed)고도, 또는 불을 초래한다(cause)고도 생각할 수 없기 때문. - 법칙성과 다른 개념의 연관은 특정한 경우에만(ad hoc) 존재하는 것으로 보임.
반환원주의(Antireductionism)
- 반환원주의는 자연법칙이 있다고 주장하므로 반실재주의가 아님.
- 반실재주의의 입장들
– 팀 마우들린(Tim Maudlin): 초기 상태(primitive status)로서 법칙성과 존재론적 초기 상태로서 법칙 긍정. 법칙은 물리적 가능성을 정의하고, 법칙에 기반한 반사실적 조건과 설명 해석 제시.
– 존 캐롤(John Carroll): 법칙성을 인과/설명적 개념으로 제시. 법칙은 우연적이지 않고 일치(coincidence)하지 않음. ‘순금 구의 지름이 1,000 마일보다 작다’는 명제는 참인 일반화이면서 적절히 일반적이지만, 일치하지 않음. 자연 안의 초기 조건에 어긋나는 일반화는 법칙이 될 수 없음.
– 마크 랭(Marc Lange): 안정성(stability)에 대한 반사실적 개념으로 법칙 설명. 그 집합과 일관된 어떤 선행조건을 추가하더라도 그 원소들이 참으로 남아 있는 집합인 경우라면, 그리고 그 경우에만, 참인 명제들로 구성된 논리적으로 닫힌 집합을 안정적이라고 부름. 준법칙적 사실들의 집합은 결코 우연적 참을 담지할 수 없음.
– 안정성 예시: ‘이 방에 모두가 앉아 있다’는 명제는 ‘누군가 ‘불이야!’라고 소리쳤다’라는 명제가 추가되는 경우 안정적인 집합이 될 수 없음. - 반환원주의에 대한 비판은 수반에 대한 비판과 유사. 우주의 단일성을 설명하는 초기 법칙에 대한 설명이 불가능하다는 근거.
귀납(Induction)
- 굿맨(Goodman), “우연적 진술과는 다르게, 오직 ‘법칙 같다(lawlike)’─그것의 진위와는 별개로 과학적 중요도만 놓고 볼 때─는 진술만이 어떤 사례에서 확증할 수 있다.
– 자연 법칙과 우연적 진리의 차이점이 불가해적인 귀납의 문제와 연관된다고 주장. - 확증성: 어떤 일반화가 우연적이고 법칙 같지 않다면 그 사례 중 하나로부터 확증할 수 없음.
– 동전 던지기 사례: 동전 던지기에서 아홉 번 윗면이 나왔을 때 열 번째에 윗면이 나오리라는 [수학적 확률 아닌] 일반화의 가능성은 높아짐. 그러나 이 가능성은 설령 참이더라도 법칙 같지 않음. ‘법 같음’을 위해 필요한 것은 시행되지 않은 사례들의 일반화가 필요함.
– 셋째 아들의 사례: 100명의 남성을 모아 놓고 50명에게 ‘셋째 아들이 있느냐’고 물었을 때, 그들 모두가 ‘그렇다’고 대답했다면 오히려 ’51번째 사람에게 셋째 아들이 있을 것’이라고 기대감을 조금이라도 높이는 것이 이성적. - 귀납적 확증에서 일반화의 역할
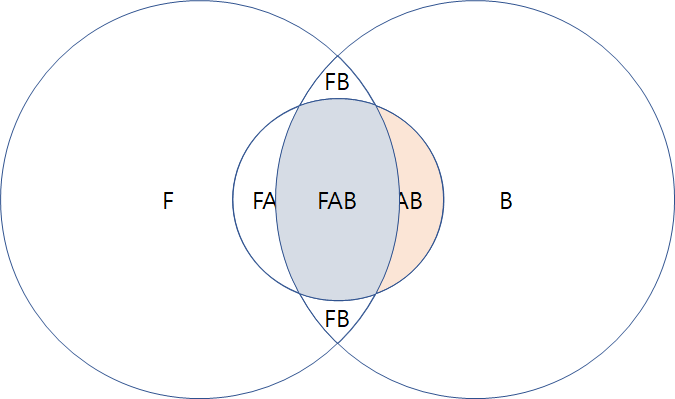
– 우연적이라고 믿어지는 일반화는 확증할 수 없음. 특정한 반사실적 참이 반드시 가져야 할 확증과 법칙 사이의 대안적 연결. F이면서 B인 As의 관찰은, F 아닌 As가 Bs라고 확증한다, As가 F가 아니더라도 여전히 A와 B인경우에만.
– 랭의 확증 개념 확장: 법칙 같은 것으로 빋어지는 일반화만 귀납적으로 확증 가능.
- 흄적 법칙 분석 비판
– 프레드 드레츠케(Fred Dretske)와 암스트롱, “귀납적 추론이 최고의 설명을 위한 추론에 기여한다.”
– 귀납적 추론의 양식: 일반화의 사레들 관찰 → 상응하는 법칙 추론 → 일반화나 발견되지 않은 사례들에 대한 추론으로 결론.
– 흄적 법칙은 최고의 설명을 추론하기 위해 요구되는 조건들을 설명하는 데 적합하지 않음. - 귀납적 추론의 한계
– 흄적 법칙은 확증된 사례가 될 수 없으나 보편자로서 법칙(law-as-universals)은 될 수 있는 것으로 보임.
– 우연적으로 알려진 일반화들도 그 사례들에 따라 확증될 수 있음.
– 가정이나 검증되지 않은 사례에 대한 확증은 어떤 배경 믿음이 형성됐는지에 민감.
필연성(Necessity)
- 자연법칙을 이해하는 기존의 관점
– 우연적 진리가 자연 법칙이 (될 수) 있음.
– “F-ness와 G-ness의 필연적 연결이 없다고 하더라도, 모든 Fs가 Gs일 때 G가 아니면서 F인 개별자가 가능하다.” - 필연성을 인정하는 주장
– 관성 법칙의 예: 뉴턴 법칙이 적용되는 가능세계에서는 관성 법칙이 참이고, 관성체가 가속 중인 세계는 관성 법칙이 거짓인 세계이다. 후자의 세계는 관성이 예화되었지만 등속이 필연화되지는 않은 세계이다.
– 어떤 필연론자들은 모든 법칙이 필연적 참이라고 주장. 다른 이들은 어떤 법칙은 보편자에 대한 단일한 진술이므로 어떤 법칙들은 우연적으로 참이라고 주장하기도 함. F-ness가 존재하지 않는다면 F-ness/G-ness 법칙이 거짓일 수 있음. - 법칙이 두 속성들 간의 필연적 관계에 의존하지 않는 두 가지 이유
– G 아닌 F가 존재하는 세계가 있더라도 모든 Fs가 Gs인 가능세계의 법칙이 가능함.
– 후험적(a posteriori)인 방법으로만 발견되는 법칙이 있음.
– 후험적으로 필연적인 참을 밝히려는 솔 크립키(Saul Kripke)의 시도: 어떤 법칙들의 후험적 본질은 그 법칙성을 위해 속성 간의 필연적 연결을 요구함.
– 필연주의는 경향은 본질적으로 인과 능력을 갖는다는 경향 이론에 따른 귀결. - 필연론의 약점
– 어떤 법칙은 우연적이라는 사실을 거부하기 어려움.
– 경향은 자연 법칙의 지지를 받는 반사실문을 유지하기 어려움.
물리학과 특수과학(the Special Sciences)
예외없는 규칙과 물리학의 관계
- 엄격한(strict) 일반화와 제한된(ceteris paribus) 일반화의 구분
– 엄격한 일반화는 ‘모든 관성체는 가속하지 않는다’와 같이 보편적 일반화로서 ‘가속하는 관성체’처럼 하나의 반례에 의해서도 모순됨. 제한된 일반화는 ‘흡연은 암을 유발한다’와 같이 조금 덜 형식적으로 보이는 일반화로서 ‘결코 암에 걸리지 않는 흡연자의 사례’로 일관성을 유지함.
– 표면적으로 ‘제한성’을 언표하지 않더라도 암시적으로는 제한성을 포함하고 있기 때문에 현실에서는 이 둘을 구분하기 매우 어려움. - 엄격한 일반화의 어려움
– 대부분의 철학자들은, 과학자들이 예외 없는 규칙 즉 법칙을 찾아내면 기초 물리학의 목적을 달성했다고 평가함.
– 카트라이트의 뉴턴의 중력 법칙은 F = Gmm/r2이지만, 이외에도 수많은 변수가 있으므로 예외 없는 규칙이 될 수 없음. 중력 원리에 대한 진술은 ‘Gmm’/r2‘을 참으로 만들기 위해 수정될 수 있지만 설명적 능력(explanatory power)을 잃게 됨. 그러므로 ‘다른 힘이 작용하지 않는다면’이라는 단서를 추가해야 함.
– 랭의 금속 막대 사례: 금속 막대의 온도는 길이와 시간에 따른 법칙 L = kL0T를 따르지만 누군가 망치로 막대를 치고 있는 경우에는 이 법칙이 적용되지 않으므로 단서를 추가해야 함.
– 엄격한 일반화는 제한적 일반화와 차이 없게 됨. - 엄격한 일반화의 문제 해결 시도
– 낸시 카트라이트(Nancy Cartwright)의 주장, “법칙은 예외 없는 규칙이 아니라 인과 능력을 기술하는 진술이다.”
– 랭의 주장, “예외 없는 규칙을 믿지 않아야 법칙으로 받아들여진 명제가 있을 수 있다.”
– 카트라이트의 주장을 심화한 기어의 주장, “법칙 진술은 단서나 제한 조항을 암시하지 않아야 하므로, 이 세상에 법칙은 없다.” - 예외 없고 법칙적인 규칙들 긍정
– 존 어만(John Earman)과 로버츠, “기초 물리학의 전형적인 이론은 ‘만약 그게 참인 경우, 정확한 단서가 필요 없는 법칙이 있을 것이다’라는 구조임. 아인슈타인의 중력장 법칙은 시공간의 리치(Ricci) 곡률텐서가 질량-에너지에 대한 전체 운동량-에너지 텐서에 적절할 것을 주장한다.”
– 중력 법칙에 관한 문제는, 중력 원리가 두 질량체 사이의 ‘중력적 힘(the gravitational force)’만을 기술한다고 이해함으로써 해결 가능. 금속 막대에 관한 문제는 법칙은 외부의 영향을 받지 않는다는 단 하나의 단서만 가져도 된다고 승인함으로써 해결 가능.
특수과학의 법칙화 가능성
- 기초 물리학이 아닌 과학의 목적도 예외 없는 규칙을 찾는 것인가? 그 과학자들은 성공할 가능성이 있는가?
– 경제학에서 수요-공급 법칙: 해당 법칙이 적용되지 않는 경우도 있으므로, 참인 법칙이 되기 위해서는 제한 조항(ceteris–paribus clause)이 필요함.
– 제리 포더(Jerry Fodor)의 특수 과학(special science): 물리적 조건 등 특수 과학의 제한적 일반화를 손상시키고 그들 스스로는 특수 과학이라 불릴 수 없는 제한 조건이 필요할 가능성이 높음.
– 도널드 데이빗슨(Donald Davidson)의 정신 인과: 제한된 심신 법칙을 반박. 그러한 법칙의 부재는 정신적 사건이 물리적 사건의 원인이 되는지 여부와 관련된다고 주장. 실제에 관한 문제를 다루는 특수 과학 긍정. - 단서의 문제가 의존하는 세 가지 기본적인 문제들
– 본질적으로 필연적 참을 완성하는 법칙이 되는 것은 무엇인가 하는 질문이 제기됨. “P는 …한 경우에, 그리고 그 경우에만 법칙이 된다.” P가 엄격하거나 제한된 일반화인지 여부에 상관 없이 모든 P에 해당되어야 함.
– 진리 조건의 일반화 문장에 대해 과학자들의 검증 필요.
– 과학자들에 의해 문장으로 표현된 일반화들 중 어떤 것이 참인가에 대한 후험적이고 과학적인 질문이 제기됨. - 맥락 감수성
– 단서의 문제는 맥락 효과에 주목하지 않은 결과.
– 어떤 경제학자가 ‘경제학적 조건 아래 엄격하게 일반화했다’고 하는 경우 맥락에 영향을 받는 요소가 진리 조건에 영향을 주었을 것.
– 같은 문장도 다른 맥락에서 언급되는 경우 명백히 거짓인 언급으로 귀결될 수 있음.
– 문장의 언어적 의미나 친숙한 규칙의 해석이 진리 조건의 변화를 야기하도록 기능할 수 있음. - 제한적 단서와 엄격한 일반화의 관계
– 제한적 단서는 엄격한 일반화가 거짓임을 보여주지 않음.
– 교수와 제자의 사례: 교수가 ‘금속 막대가 가열됐을 때 열 변화는 막대의 길이에 비례한다’고 할 때 제자가 ‘누군가 막대에 망치질 하고 있지 않은 경우’를 제시했다 하더라도 교수의 언급이 거짓으로 되는 것은 아님.
– 제자가 제시한 사례는 교수의 사례과 무관함. 교수의 문장은 참이 되기 위해 제한 조항을 암시할 필요 없음.
– 일반적인 대화에서는 제한적 일반화 문장이 모든 가능한 경우를 아우르지 않음. - 특수 과학과 엄격한 일반화의 관계
– 특수 과학에서 엄격한 일반화를 시도하는 경우 특수 과학의 법칙성은 부정될 수 있음. 이러한 특성은 법칙성의 다른 조건들과는 다르게, 특수 과학의 일반화에서 참이 됨.
자연 법칙 이론의 이후 전개
다섯 가지 방향으로 전개됨
- 법칙이 우주를 지배하는지, 법칙성을 이해하는 데에는 어떻게 영향을 주는지에 대한 연구.
- 법칙성이 과학 이론의 일부 내용인지 여부에 대한 연구.
– 과학 이론은 인과 관계와 많이 연계됐으나 법칙성과는 그렇지 않았음.
– 로버츠의 비유: 유클리드 기하학에서 ‘두 점 사이를 잇는 것은 선’이라고 했을 때, 그것은 가정이지만, 유클리드 기하학에 포함되는 가정은 아니다. 유클리드 기하학은 가정에 관한 이론이 아니라 점, 선, 면에 관한 이론이기 때문이다. - 우연적인 자연 법칙이 있는지 여부에 대한 연구.
- 법칙이 설명할 수 있는 범위는 어디까지인지에 대한 연구.
- 무엇이 법인지 보고하는 언어와 법칙 그 자체를 표현할 때 사용하는 언어에 대한 연구.